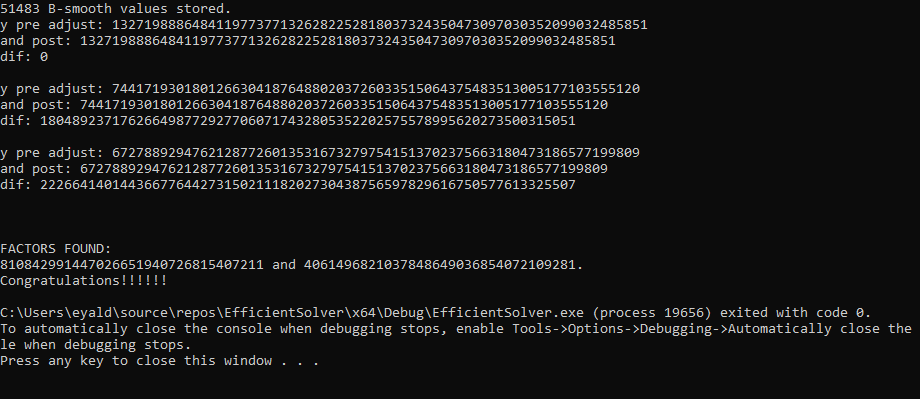
Implemented Carl Pomerance’s quadratic sieve factorization algorithm in order to break RSA encryption using a 233-bit (70-digit) public key. Written in C++, this program utilized methods such as the Euclidean algorithm, timed Pollard rho tests to filter out unlikely B-smooth values, the Shanks-Tonelli algorithm to calculate modular square roots, log division optimizations, multithreading, parallelization across multiple systems, MeatAxe to solve linear algebra problems on large sparse matrices, and efficient Legendre symbol calculations using the law of quadratic reciprocity.

Through the use of parallelization and of optimizations with fine-tuned benchmarked parameters, real-time runtime was reduced from several months to six days.